In today’s marketplace, audio power amplifiers are conventionally viewed as voltage sources, delivering a given voltage at the output that is a multiple of an input voltage. To the extent that they are truly voltage sources, having a very low output impedance, they simply deliver whatever current happens to reflect the response of the loudspeaker to the defined output voltage.
Recently I have been playing with current source power amplifiers that have high output impedances and deliver a specific current to the load in response to an input voltage. The voltage across the loudspeaker reflects its response to this defined current. You could say that we have swapped the words voltage and current.
In a previous article, “Current Source Amplifiers and Sensitive / Full-Range Drivers”, I have discussed some advantages with these amplifiers for Lowther, Fostex, and similar loudspeakers. In these cases the loudspeaker driver was “full-range”, so there was no need for a crossover network to apportion the frequency spectrum between different drivers. However I have found that these drivers typically appreciated a finite source impedance and often benefit from some equalization in the upper midrange and high frequencies.
With a voltage source amplifier equalization is usually applied by a network in series with the driver. With a current source it is usually applied by elements placed in parallel, leaving the driver directly connected to the output terminals of the amplifier.
Of course we don’t want to limit ourselves strictly to one-driver loudspeaker systems (attractive as they may be) and so we need to consider a means of filtering the signal to divide it between the drivers. We certainly can make life easy by using an electronic crossover network that does the filtering before multiple amplifiers. This way each driver gets an amplifier to itself. This has real performance advantages, but is generally more complex and expensive than a passive crossover between the amplifier and speaker.
Voltage Source Networks
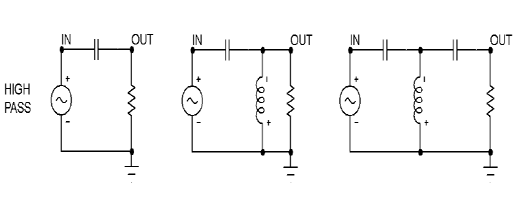
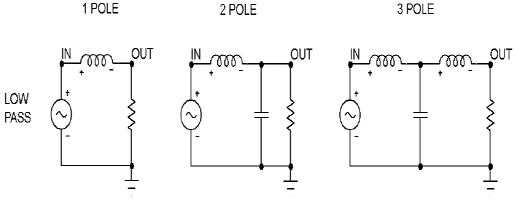
The classic crossover networks of Figure 1 work very well if you have a voltage source. Here you see both high pass (tweeter) and low pass (woofer) filters with a resistor representing the loudspeaker. Of course a real loudspeaker is not exactly a resistor, but I don’t want to get confusing here. A low pass network gradually attenuates the high frequencies as the frequency goes higher than a particular transition point called the crossover frequency. Similarly, a high pass network gradually rolls off the frequencies lower than the crossover frequency. The shapes of both types of filters can be characterized by numbers in addition to the crossover frequency, but here we will limit ourselves to discussing just the slope.
FIG 1 . CLASSIC VOLTAGE SOURCE FILTERS
In the examples of Figure 1, we see three different filters for both the high pass and the low pass filters. The first is a 1 pole filter, corresponding to a roll-off slope of 6 dB/octave. The second is a 2 pole filter, which rolls off at 12 dB/octave. The third is a 3 pole filter, which rolls off at 18 dB/octave.
There are of course filters with even more poles, and the exact shape of these filter curves can vary from sharply peaked at the “knee” of the crossover frequency to very gentle transitions. They all have different phase characteristics as well. There is no such thing as an ideal crossover network for all loudspeaker drivers, and even considerable difference of opinion as to the best for any given set of drivers.
Cautionary Comments
Everything you read here should be taken as approximate examples to help you arrive at your own filter types and values. It is rare for a “text book” filter example to be the best in any particular real life case. The best sounding crossover networks, whether active or passive are usually the result of painstaking experimentation, measurement and listening. Remember also that the typical loudspeaker driver only approximates a resistor as a load, and additionally has an acoustic output to be considered which is not very flat or phase perfect.
The decisions about what frequency or slope are your own, and you can mix and match them as you please. Occasionally you have to consider protecting a tweeter or midrange from too much power at lower frequencies, but after that you can play as you like.
Inside Out
When you switch from designing filter networks for voltage sources to networks with current sources, you will find that everything is suddenly turned inside out. Capacitors become inductors and vice versa, and “T” networks become “pi” networks and vice versa. Multiple filters that used to be placed in parallel off the amplifier’s output terminals are now strung in series. Don’t worry, we’ll get you straightened out.
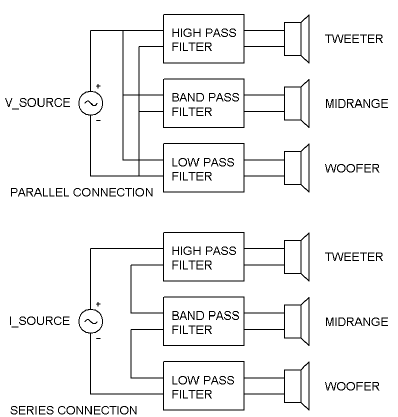
FIG 2 . PARALLEL AND SERIES FILTER CONNECTION
Figure 2 shows part of this difference. At the top we see a voltage source amplifier driving three filters and speakers in parallel to divide the audio for a woofer, midrange and tweeter. They all share the same voltage and the same ground. At the bottom, we see a current source amplifier where the filters and speakers are wired in series. They all share the same amount of current. This is a key item – that just as voltage source filters can assume a given equal input voltage, current source filters can assume equal input current. In this way, both types of filters can be designed independently so that the characteristic of one filter does not alter the characteristic of another. You can’t say the same thing about voltage source filters strung in series or current source filters run in parallel – in those cases, the specifics of each filter will influence the others, as we will see in some band pass filter examples later.
Let’s look at some filter examples. They have been constructed for matching –3 dB points at the crossover frequency, and so that they present a nearly constant impedance to the source. Having a constant total impedance allows use with voltage sources equally well. Keep in mind that with a voltage source driving networks in series, when you adjust one filter, you affect the response of the others. With a current source, the response of other filters in series is not affected.
Single Pole 2 Way Filter
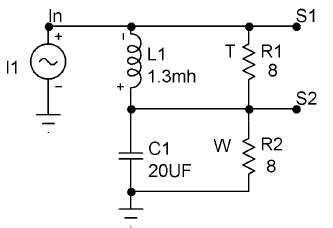
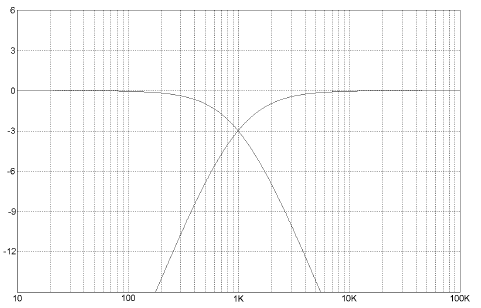
Figure 3A shows a simple current source crossover where the woofer and tweeter are crossed over each at 1 kHz and at a slope of 6 dB/octave. The values of the inductor L and capacitor C are determined by the formulas:
L = R1 / (6.28 * F) and C = 1 / ( 6.28 * R2 * F)
L is the inductance in Henries, R is the load resistance in ohms, C is the capacitance in Farads, F is the transition frequency in Hertz. By the way, the “T” and “W” in Fig 3A indicate tweeter and woofer. When you see an “M” later, it will mean midrange.
FIG 3A. 1.POLE-2WAY FILTER
Figure 3B shows the resulting response of this, the simplest filter we will see. As will be the case of all curves, the vertical axis is in decibels (dB) and the horizontal axis is frequency.
FIG 3B 1 POLE-3 WAY FILTER RESPONSE
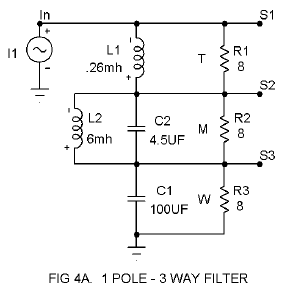
Single Pole 3 Way Filter
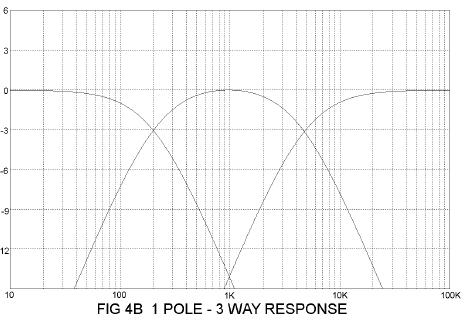
We can create a 1 pole 3 way filter easily by simply adding an additional filter in the middle for the midrange driver, as shown in Figure 4A. The formulas applying to the previous example will work perfectly for the woofer and tweeter, but the midrange filters L2 and C2 will be off slightly, depending on the proximity of the two crossover points, which in this case are 200 Hz and 5 kHz. Here the coil needs to be about 10% lower than suggested by the calculation, and the capacitance needs to be about 10% higher. This is due to the loading influence of each of these elements on the other, and the variation increases as the crossover frequencies get closer.
You can calculate this if you’re mathematically gifted, run a computer program if you can follow instructions, or try wiring in different values if you’re good with your hands. All three approaches are likely to end up with the “wiring in different values” when it comes time to evaluate the results. In this case the results are in Figure 4B.
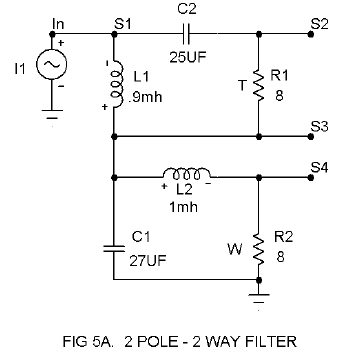
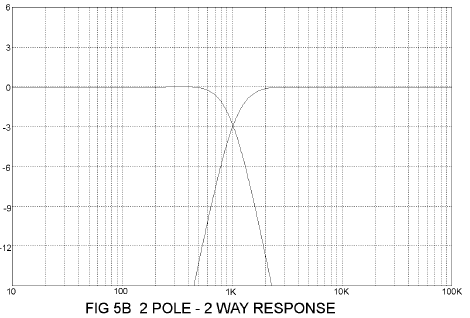
2 Pole 2 Way Filter
In Figure 5A we add another pole to each filter in the form of C2 on the high pass and L2 on the low pass, and we get the curves of Figure 5B. The formulas have changed a bit, but you can scale from the examples. Remember that the high and low pass are independently adjustable. As you vary the frequency and resistance of the load, use the following rules:
All examples of C are inversely proportional to the variation in frequency and load impedance. If you double the value of R, then you will halve the value of C. If you double the value of the frequency, you will halve the value of C. If you double the resistance and the frequency both, you will quarter the value of C.
All examples of L are inversely proportional to the variation in frequency, as with C, but they are proportional to the resistance. If you double the value of R, then you double L also.
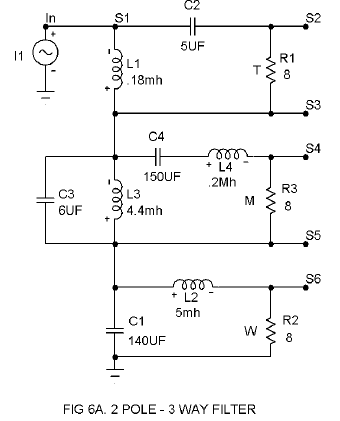
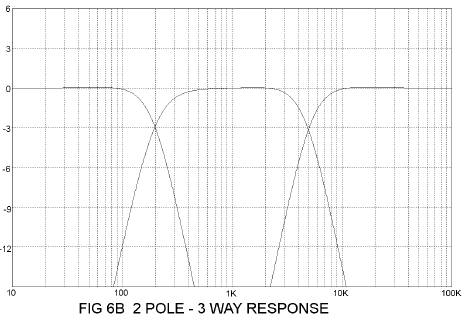
2 Pole 3 Way Filter
As with the 1 pole 3 way filter, we simply sandwich in a midrange filter in series with the high pass and low pass systems. The rules for the L and C values are the same as the 2 pole 2 way example, and of course don’t work so well for the midrange depending on the proximity of the two crossover frequencies. Like I said before, you can calculate it out exactly, but you’ll still end up fooling around with it when you actually adjust the speaker, so don’t get too excited. Figures 6A and 6B show the circuit and the resulting curves. Like all the other examples, the values of L and C scale with load resistance and frequency. Again, L is proportional to R and inversely proportional to F. C is inversely proportional to R and F.
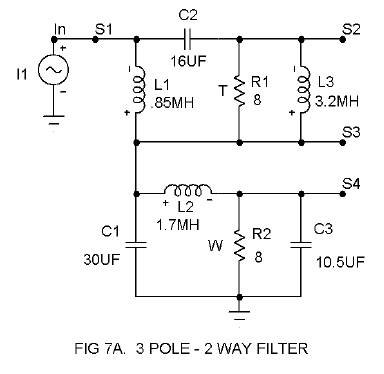
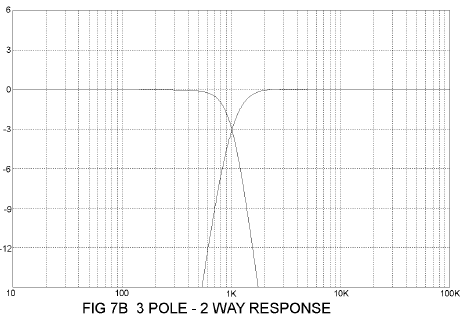
3 Pole 2 Way Filter
Now we’re starting to get into some complicated stuff as in Figures 7A and 7B. All the rules of the preceding examples apply, such as they are. For scaling, L is proportional to R and inversely proportional to F. C is inversely proportional to R and F.
This is a good time to note that there is no rule that says you have to pick the same frequencies and slopes for adjacent elements. More often than not, I use single pole slopes for midranges, 1 or 2 poles for tweeters and 2 or 3 poles for woofers. Also more often than not, I set the high and low pass portions at different frequencies. It’s strictly a matter of what works best, and that is usually not exactly the textbook version.
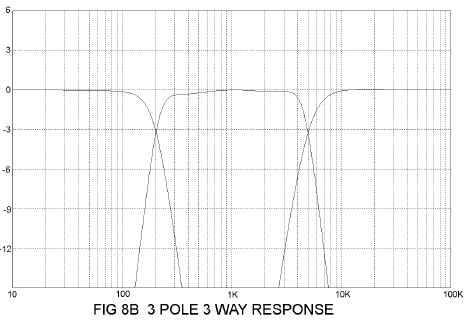
33 Pole 3 Way Filter
This is the most complex example we will look at. The high pass (tweeter) portion and the low pass (woofer) portion are L C and R scalable as previously, and as long as the midrange filter frequencies are at a ratio of 5000Hz / 200 Hz (25 to 1), then you can scale it as well. If they’re not at that ratio and you really want those slopes, be prepared for some work.
Figures 8A and 8B shows the result of my labors in this regard.
Conclusion
Filter networks in series is not a new concept, but it is not that popular because with a voltage source, anytime you adjust one filter you affect the response of the others. With a voltage source amplifier this is avoided by placing the filter systems in parallel, so that they all share the same input voltage independently of each other.
With a current source amplifier, you can use filters in series easily because they all share the same current, and adjusting the filter values in one network does not alter the response of the other filters. You can run networks in parallel off a current source, just as you can series filters with a voltage source.
As pointed out previously, the filter examples I have given have a fairly constant aggregate impedance, so you can use them as is equally well with a voltage or current source. With a voltage source, however, the moment you adjust one of the filters, you'll find yourself readjusting the others.
Current source amplifiers aren’t for everybody, although the great Malcolm Hawksford might effectively argue the case. I have certainly found that they have real charm with highefficiency full-range loudspeakers as I have detailed elsewhere. Of course the definition of “full-range” varies, and there are quite a few cases where users, myself included, have attached a sub-woofer and/or a tweeter to extend this range. If you do, you have the choice of using active electronic crossovers or passively filtering these pieces into the system.
I have successfully driven Lowthers, Fostexes, and their cousins with current source amplifiers while applying a passive single pole low pass filter to them. From there I can easily bring in a tweeter (like the TAD PT-R9 ribbon) with a passive 2 pole filter, usually at 10 KHz and above. Generally it’s been my experience that a big subwoofer like El Pipe-O prefers a voltage source for high damping, and so I have used an active filter to divide it from the fullrange speaker in the range below 100 Hz.
The more general category of limited-bandwidth high-efficiency drivers can benefit from current source amplification as well, particularly examples of high-efficiency woofers coupled with horn loaded compression drivers. This paper was an outgrowth of that investigation, which is still progressing.
In any case, we have seen that constructing crossover filters for current source amplifiers is not particularly difficult, or at least not more difficult than for voltage amplifiers. For that matter, we shall soon see that constructing a current source amplifier is not more difficult than a voltage source.
Copyright 2004 Nelson Pass
www.passlabs.com
www.passdiy.com
www.firstwatt.com
Less...